A Trigonometry Table, also known as a Trigonometric Ratios Table, is a reference tool used in mathematics to assist in calculating angles and sides of triangles. For various angles, it provides the values of the six trigonometric functions, namely sine, cosine, tangent, cosecant, secant, and cotangent. The table is organized in rows and columns, with angles listed in one column and the corresponding trigonometric ratios in the other.
Table of Contents Show
What is Trigonometry?
Trigonometry is a branch of Mathematics that studies relationships between side lengths and angles of triangles (right-angled triangles). It has a wide number of applications in other fields of Mathematics.
It helps in finding the angles and missing sides of a right-angled triangle with the help of trigonometric ratios.
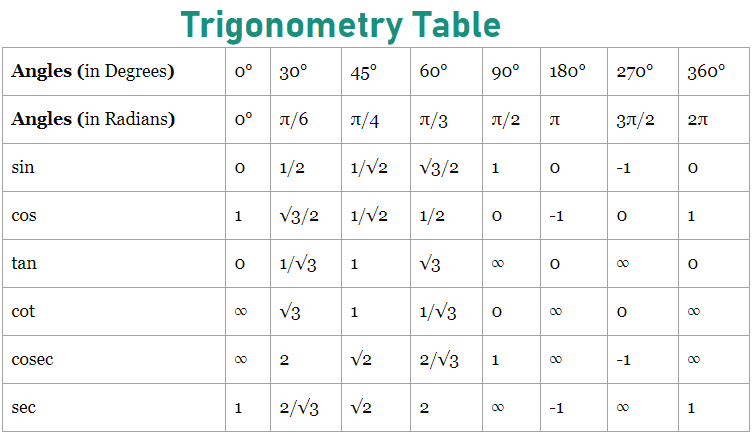
Trigonometry Table
The trigonometry table helps to find the values of trigonometric ratios of standard angles.
The table contains standard angles in degrees and radians, that are very easy to convert of degrees to radians and vice versa. Various standard angles including 0°, 30°, 45°, 60°, 90°, sometimes with other angles such as 180°, 270° and 360°.
It consists of trigonometric ratios – sine, cosine, tangent, cotangent, coscent, secant. These ratios can be abbreviated as sin, cos, tan, cosec, sec, and cot.
The value of trigonometric ratios of standard angles is required to solve trigonometric problems. Therefore, it is necessary to remember the values of trigonometric ratios of these standard angles.
Check the Trigonometry Table for trigonometric ratios, and trigonometric function values for standard angles, and Understand trigonometry table tricks.
Trigonometric Ratios Table
The trigonometric ratios table contains the value of trigonometric ratios at specific angles. These values are applicable in the right-angle triangle.
| Angles (in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (in Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Simple Trick To Remember Trigonometric Ratio Table
Remembering the values of standard angles can be difficult. But with the method described below you can easily remember the values of standard angles.
Create a table with a top row by listing angles such as 0 °, 30 °, 45 °, 60 °, and 90 °, and write all trigonometric functions in the first column such as sin, cos, tan, cot, cosec, sec.
Determining Values Of Sine Of Standard Angles
- To determine the values of sin of standard angles, Write the angles 0°, 30°, 45°, 60°, and 90° in ascending order and assign them values 0, 1, 2, 3, and 4 according to the order.
So, 0° ⟶ 0 , 30° ⟶ 1, 45° ⟶ 2 , 60° ⟶ 3 , 90° ⟶ 4
- Then divide the values by 4 and square root the entire value.
√(0/4)=0, √(1/4)=1/2, √(2/4)=1/√2, √(3/4)=√3/2, √(4/4)=1
Now for the remaining three Formula
- sin (π − θ) = sin θ
- sin (π + θ) = -sin θ
- sin (2π − θ) = -sin θ
Here, π=180°
- sin (180°− 0°) = sin (180) = sin 0° = 0
- sin (180° + 90°) = sin (270°) = -sin 90° = 1
- sin (360°− 0°) = sin (360°) = -sin 0° = 0
Now you will remember the Trigonometry Table for Sin like:
Trigonometry Table for Sin
| Angles (in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (in Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
Determining Values Of Cosine Of Standard Angles
- To determine the values of cos of standard angles, Write the angles 0°, 30°, 45°, 60°, 90° in ascending order and assign them values 4, 3, 2, 1, 0 according to the order.
So, 0° ⟶ 4, 30° ⟶ 3, 45° ⟶ 2, 60° ⟶ 1, 90° ⟶ 0
- Then divide the values by 4 and square root the entire value.
√(4/4)=1, √(3/4)=√3/2, √(2/4)=1/√2, √(1/4)=1/2, √(0/4)=0
Now for the remaining three Formula
- cos(π−θ) = -cosθ
- cos(π+θ) = -cosθ
- cos(2π−θ) = cosθ
Here, π=180°
- cos (180°− 0°) = cos (180) = -cos 0° = -1
- cos (180° + 90°) = cos (270°) = -cos 90° = 0
- cos (360°− 0°) = cos (360°) = cos 0° = 1
Now you will remember the Trigonometry Table for Cos like:
Trigonometry Table for Cos
| Angles (in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (in Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
Remember Trigonometry Formulas
Remember these trigonometry formulas to determine Values of other ratios:
- sin θ= cos (90° – θ)
- cos θ= sin (90° – θ)
- tan θ = sin θ/cos θ = 1/cot θ = cot (90° – θ)
- cot θ = cos θ/sin θ = 1/tan θ = tan (90° – θ)
- sec θ = 1/cos θ = cosec (90° – θ)
- cosec θ = 1/sin θ = sec (90° – θ)
Determining Values Of Tangent Of Standard Angles
tan θ = sin θ/cos θ
Hence, the tan row can be generated.
Trigonometry Table for Tan
| Angles (in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (in Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| Tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
Determining Values Of Cotangent Of Standard Angles
cot θ = cos θ/sin θ
Hence, the tan row can be generated.
Trigonometry Table for Cot
| Angles (in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (in Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
Determining Values Of Secant Of Standard Angles
sec θ = 1/cos θ
Hence, the tan row can be generated.
Trigonometry Table for Sec
| Angles (in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (in Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sec | 0 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | -1 |
Determining Values Of Cosecant Of Standard Angles
cosec θ = 1/sin θ
Hence, the tan row can be generated.
Trigonometry Table for Cosec
| Angles (in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (in Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
Trigonometry Table | Trigonometric Ratios Table (Image)
Check This Calculator:
Click Here ▷ Square of Numbers From 1 to 100
